컴퓨터에서 표현되는 진법인 2진수, 8진수, 10진수, 16진수에 대해 알아본다.
아래는 각 진법의 표현 방법이다.
| 10진수(Decimal) | 2진수(Binary) | 8진수(Octal) | 16진수(Hexadecimal) |
| 0 | 0000 | 0 | 0 |
| 1 | 0001 | 1 | 1 |
| 2 | 0010 | 2 | 2 |
| 3 | 0011 | 3 | 3 |
| 4 | 0100 | 4 | 4 |
| 5 | 0101 | 5 | 5 |
| 6 | 0110 | 6 | 6 |
| 7 | 0111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
표에서 보는 바와 같이 10진수는 우리가 실생활에서 보는 친숙한 진법이고, 2진수는 0과 1로만 표현하는 컴퓨터가 이해 할 수 있는 진법이다. 8,16진법은 자리수당 2^3, 2^4 만큼 표현이 가능해 2진수를 직관적으로 변환이 가능하다는 특징이 있다.
이제 각 진법별 변환 방법에 대해 알아보겠다.
2진수
(1) 8진수
3비트씩 1자리수로 끊어서 10진수로 변환한 후 각 자리수로 표현한다.
ex) 10110011(2)를 8진수로 변환
| Binary | 010 | 110 | 011 |
| Octal | 2 | 6 | 3 |
각 자리수를 10진수로 변환 후 합치면 8진수 263이라는 값이 나왔다.
(2) 16진수
4비트씩 1자리수로 끊어서 10진수로 변환한 후 각 자리수로 표현한다.
ex) 10110011(2)를 16진수로 변환
| Binary | 1011 | 0011 |
| Hexadecimal | B(13) | 3 |
각 자리수를 10진수로 변환 하였을 때 13과 3이라는 값이 나온다. 여기서 13은 16진법으로 변환하면 B가 되므로 결과는 16진수 B3라는 값이 나왔다.
(3) 10진수
우측부터 2^(n-1) (n은 자리수)을 모두 더한다.
ex) 10110011(2)를 10진수로 변환
| Binary | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| Decimal | 128 (2^7) | 0 (2^6) | 32 (2^5) | 16 (2^4) | 0 (2^3) | 0 (2^2) | 2 (2^1) | 1 (2^0) |
위 표와 같이 각 자리수에서 이진수 1로 표현된 숫자를 모두 더하면 된다.
128 + 0 + 32 + 16 + 0 + 0 + 2 + 1 = 179(10)
8진수
(1) 2진수
각 자리수를 2진수로 변환하여 3비트로 표현하고 나온 결과를 나열한다.
ex) 654(8)를 2진수로 변환
| Octal | 6 | 5 | 4 |
| Binary | 110 | 101 | 100 |
각 자리수를 2진수로 변환하면 110, 101, 100가 나온다. 나온결과를 나열하면 2진수 110101100 라는 값이 나왔다.
(2) 16진수
선행으로 2진수로 변환하고 나온 결과에서 4비트씩 끊어 16진수로 표현한다.
ex) 654(8)를 16진수로 변환
8진수 654는 앞서 110101100의 결과가 나왔다.
| Binary | 0001 | 1010 | 1100 |
| Hexadecimal | 1 | A(12) | C(14) |
2진수 110101100을 4비트씩 끊으면 0001, 1010, 1100이 나온다. 이를 표현하면 16진수 1AC가 나온다.
(3) 10진수
우측부터 8^(n-1) (n은 자리수)을 모두 더한다.
ex) 654(8)를 10진수로 변환
| Octal | 6 | 5 | 4 |
| Decimal |
(8^2) | (8^1) | (8^0) |
| 64 X 6 = 384 | 8 X 5= 40 | 1 X 4 = 4 |
384 + 40 + 4 = 428
각 자리수를 모두더하면 10진수 428의 값이 나왔다.
10진수
(1) 2진수
10진수의 숫자가 2보다 작을 때까지 2로 나누고 나눌때 마다의 나머지를 최근순서대로 조합한다.
ex) 47(10)을 2진수로 변환
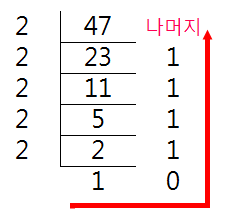
위와 같이 10진수 47을 2로 나눠 마지막 몫과 나머지를 조합하여 2진수 101111의 결과가 나왔다.
(2) 8진수
10진수의 숫자가 8보다 작을 때까지 8로 나누고 나눌때 마다의 나머지를 최근순서대로 조합한다.
ex) 47(10)을 8진수로 변환

위와 같이 10진수 47을 8로 나눠 마지막 몫과 나머지를 조합하여 8진수 57의 결과가 나왔다.
(3) 16진수
10진수의 숫자가 16보다 작을 때까지 16로 나누고 나눌때 마다의 나머지를 최근순서대로 조합한다.
ex) 47(10)을 16진수로 변환

위와 같이 10진수 47을 16으로 나눠 마지막 몫과 나머지를 조합하여 16진수 2F의 결과가 나왔다.
16진수
(1) 2진수
각 자리수를 2진수로 변환하여 4비트로 표현하고 나온 결과를 나열한다.
ex) F6(16)을 2진수로 변환
| Hexadecimal | F(15) | 6 |
| Binary | 1111 | 0110 |
각 자리수를 2진수로 변환하면 1111, 0110이 나온다. 나온결과를 나열하면 2진수 11110110 값이 나왔다.
(2) 8진수
선행으로 2진수로 변환하고 나온 결과에서 3비트씩 끊어 8진수로 표현한다.
ex) F6(16)을 8진수로 변환
16진수 F6은 앞서 11110110의 결과가 나왔다.
| Binary | 011 | 110 | 110 |
| Octal | 3 | 6 | 6 |
2진수 11110110을 3비트씩 끊으면 011, 110, 110이 나온다. 이를 표현하면 8진수 266이 나온다.
(3) 10진수
우측부터 16^(n-1) (n은 자리수)을 모두 더한다.
ex) F6(16)을 10진수로 변환
| Hexadecimal | F | 6 |
| Decimal |
(16^1) | (16^0) |
| 16 X 15=240 | 1 X 6 = 6 |
240 + 6 = 246
각 자리수를 모두더하면 10진수 246의 값이 나왔다.
이상으로 진법간 변환방법에 대해 알아보았다.
* CopyRight 2021. Jay Park All rights reserved.
'ETC > ETC' 카테고리의 다른 글
| [E-Mail] 메일 보안 필터링 이론 정리 (0) | 2022.04.06 |
|---|---|
| [E-Mail] 이메일 시스템 구조 및 용어 정리 (0) | 2022.03.01 |
| [E-Mail] Telnet과 OpenSSL을 이용한 SMTP 메일 발송 (0) | 2022.02.03 |
| [Web] 웹 데이터 수집 및 가공 관련 용어정리 (0) | 2021.09.13 |
| [ETC] 함수와 관련 용어 정리 (0) | 2021.09.13 |